283

Behold, a square (sopuli.xyz)

submitted 3 weeks ago by hydroptic@sopuli.xyz to c/science_memes@mander.xyz

30 comments fedilink hide all child comments

Source

top 30 comments

sorted by: hot top controversial new old

[-] spankmonkey@lemmy.world 158 points 3 weeks ago

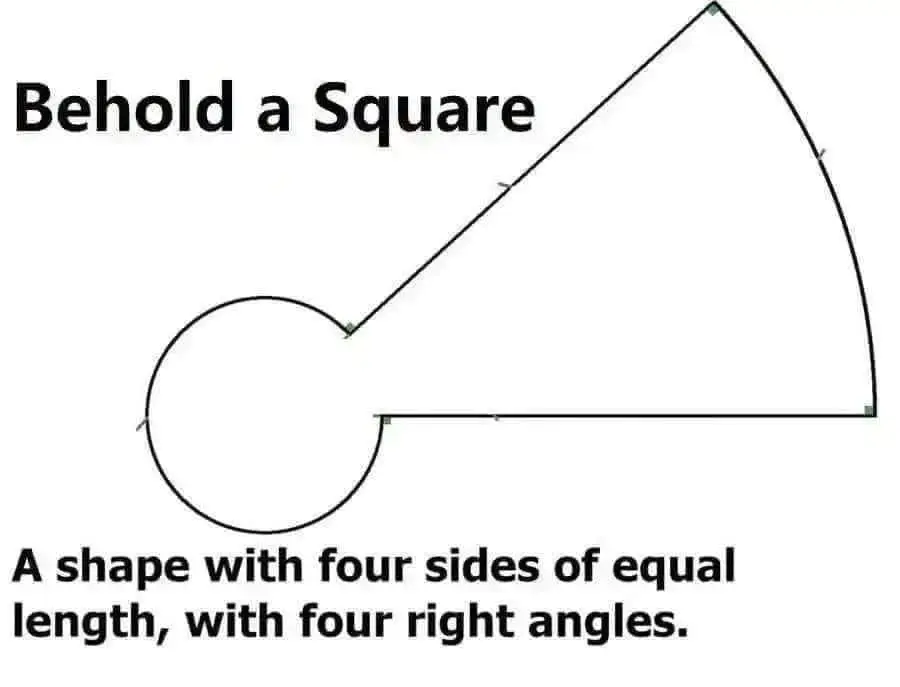
As long as we ignore the parallel sides requirement, sure.

[-] kryptonianCodeMonkey@lemmy.world 96 points 3 weeks ago

And that the 90 degree angles should be interior angles.

[-] ninja@lemmy.world 49 points 3 weeks ago

And that polygons should only consist of straight lines.

[-] bstix@feddit.dk 38 points 3 weeks ago

Yes sure, in Euclidean geometry, but this is clearly keyhole shaped geometry.

[-] rain_worl@lemmy.world 1 points 2 weeks ago

geodesics

[-] wolfpack86@lemmy.world 11 points 3 weeks ago

They're also not actually right angles, as the curvature starts departing from the angles origin. They may be approximately 90, down to many many small decimal places, but they are not 90.

[-] kryptonianCodeMonkey@lemmy.world 29 points 3 weeks ago* (last edited 3 weeks ago)

That's not accurate. If you are measuring the angle of a line intersecting with a curved surface, you measure against the tangent at the point of contact/intersection. It can be and still is exactly 90 degrees.

[-] Prunebutt@slrpnk.net 36 points 3 weeks ago

Take shitposts seriously and point out their obvious errors

-Carl Friedrich Gauss, probably

[-] Eheran@lemmy.world 22 points 3 weeks ago

Science memes is not r/shitposting? I would assume the person is serious when posting here.

[-] rain_worl@lemmy.world 4 points 3 weeks ago

gasp!!! it is c/!!!

[-] hydroptic@sopuli.xyz -5 points 3 weeks ago

I would assume the person is serious when posting here.

This sounds like a "you" problem

[-] Tja@programming.dev 4 points 3 weeks ago

The name of that Gauss?

Ampere

[-] lugal@sopuli.xyz 22 points 3 weeks ago

c/gatekeeping squares

[-] hydroptic@sopuli.xyz 10 points 3 weeks ago

You're no fun

[-] Tolookah@discuss.tchncs.de 5 points 3 weeks ago

Polar coordinate square?

[-] Lemjukes@lemm.ee 32 points 3 weeks ago

I remember enough from geometry to know this is horseshit and be annoyed at it but not enough to actually prove why

[-] Tja@programming.dev 11 points 3 weeks ago

Sides must be straight and parallel two and two.

[-] OldChicoAle@lemmy.world 3 points 3 weeks ago

QED

[-] Doll_Tow_Jet-ski@fedia.io 11 points 3 weeks ago

What are the 4 sides?

[-] Assman@sh.itjust.works 17 points 3 weeks ago

The black lines

[-] CodexArcanum@lemmy.world 8 points 3 weeks ago

The semi-circle is one side, then the 2 straight edges, and the arc between them is the 4th side.

[-] Doll_Tow_Jet-ski@fedia.io 7 points 3 weeks ago

That's what I thought. The only way on which this has four sides is if the semi -circle is a side. But if that's the case, then I don't know wha the definition of "side" is

[-] bstix@feddit.dk 9 points 3 weeks ago

Knock knock. Do you have a moment to discuss non-euclidean geometry?

[-] Doll_Tow_Jet-ski@fedia.io 10 points 3 weeks ago

/slams door

[-] UrLogicFails@beehaw.org 5 points 3 weeks ago

Someone may want to double-check my math on this one, but the length of the sides will be dependant on the radius of the smaller circle

ϴ=π+1-√(π^2+1), l=(2π-ϴ)r_1, l is the length of the sides. r_1 is the radius of the smaller circle

[-] m0darn@lemmy.ca 4 points 3 weeks ago* (last edited 3 weeks ago)

I look at your diagram and see:

ϴ= L/(L+R)

And

2π-ϴ = L/R

I solved those (using substitution, then the quadratic formula) and got

L= π-1 ± √(1+π²) ~= 5.44 or -1.16

Whether or not a negative length is meaningful in this context is an exercise left to the reader

Giving (for L=5.44):

ϴ~= 0.845 ~~48.4°

I'm surprised that it solved to a single number, maybe I made a mistake.

[-] UrLogicFails@beehaw.org 3 points 3 weeks ago

That lines up pretty similarly with what I found also. The angle should be a constant since there is only one angle where the relationship would be true. I just left it in terms of π because I try to avoid rounding.

Having said that, L would be a ratio of r; which I think lines up with what you found as well.

[-] affiliate@lemmy.world 11 points 3 weeks ago

it’s homeomorphic to a square, so why not

[-] hydroptic@sopuli.xyz 4 points 3 weeks ago

See, you get it

[-] davidagain@lemmy.world 2 points 1 week ago

I'll tell you why not! You hippie homeopaths are all the same! Science has scienced the evidence that there's no evidence for homopathic medicines otter than the libido effect.