aetheriumslinky

Crap, I wrote a long comment and accidentally closed the tab. Well.

In a nutshell: 15 ramp spells is doable. There are already 15 colourless rocks to fulfill this order.

So the analysis above doesn't take average mana value into account. It simply looks at the (subjectively) acceptable starting hands and goes from there. You can indirectly manipulate the assumed average mana value by modifying which hands to accept and which to mulligan.

I have experimented with a variable MV setup... But the results are pretty wild. I'll return to you if I ever get around to doing some more of that. (Yeah, that's going to be tonight lol.)

Images:

No mulligans, general advice (first post):

Three mulligans, general advice (first post):

Accepting 4 land hands, general advice (first post):

4-mana commander (second post):

SECOND POST:

My commander costs 4 mana. How many lands and ramp spells do I need to get it out on turn 3? TL;DR: 37 lands and 15 ramp spells at mana value 2 or less.

This short analysis is a continuation to "I'll just cut a land": A statistical analysis of lands and ramp in EDH article that was published 7 months ago. Also provocative title: I'm not saying this is the absolute truth but I'm putting forth the idea that every deck does need enough mana sources to play the game. This article discusses 4 mana commanders being cast ahead of curve.

I was building a new deck, helmed by Rosheen Meanderer (scryfall). The thing about Rosheen X-creatures is that I need Rosheen out as soon as possible (turn 3 or earlier). My prior advice was 36 lands and 12 ramp spells (see the other Reddit article) but I was left wondering if that's enough to get Rosheen out on turn 3. Answer: it's not.

This time I used a bit more complicated method of simulating the game to turn 2 assuming we're not playing any draw/loot/filter/rummage spells in the first two turns (which is true for my deck). The "simulation" here is simply to see a decent hand and hope our next two draws are good.

Why turn 2? If you play a Rampant Growth on turn 2 you can still cast your 4-mana commander on turn 3. If your 3rd draw is a Rampant Growth, however, it doesn't help you at all. Thus we need to cast all our ramp spells by turn 2. This also incidentally means that your ramp at mana value 3 or above doesn't help you cast your commander at all so you shouldn't count those towards ramp in your deck when it comes to this analysis. Cultivate is a decent card but exclude it this time.

The math is based on opening hands. Here's a table of hands and early draws I deemed acceptable:

opening 7 lands opening 7 ramp first 2 draws lands first 2 draws ramp 2 1 1 or 2 0 or 1 2 2 1 or 2 0 3 0 0 or 1 1 or 2 3 1 0 or 1 0 or 1 3 2 0 or 1 0 4 0 0 1 or 2 4 1 0 0 or 1 The philosophy here was that I draw a relatively safe hand and taking the two draws into account we're looking at 4 mana on turn 3. In other words that's our "mana target". There may also be a surplus left over since drawing into 4 lands is not necessarily a bad thing looking into the future. Looking at a 5 land opener can be a good thing but if there's a ramp spell in it it means we've only got one more spells that we can play (7-5-1=1). Doesn't sound nice to me. But in general I don't mind an extra land or ramp spell to be cast on turn 4. Feel free to disagree with my "safe" openers.

Obviously we can't know the future draws so they only act as "weight factors" for each hand. If you draw into a land rich hand with no ramp you absolutely need that one ramp spell. While we're optimising for a land rich hand by including it in the table we also take into account the fact that there must be a ramp spell in the next two cards which in turn increases the number of ramp spells needed in the deck so they kind of counteract each other.

Think of it this way: 3 lands and 1 ramp is a very, very safe hand. If it can accept any outcome from future draws it's the "best" opener possible. It gets a weight of 1 because the probability of drawing any (follow-up) card from your deck is always 1. If your hand is 2 lands and 1 ramp spell your hand must draw an extra land to survive - draws with no lands are bad so we exclude them and thus lower the weight of the hand in terms of overall optimisation. This way the math prefers the safest hands and gives them a higher priority.

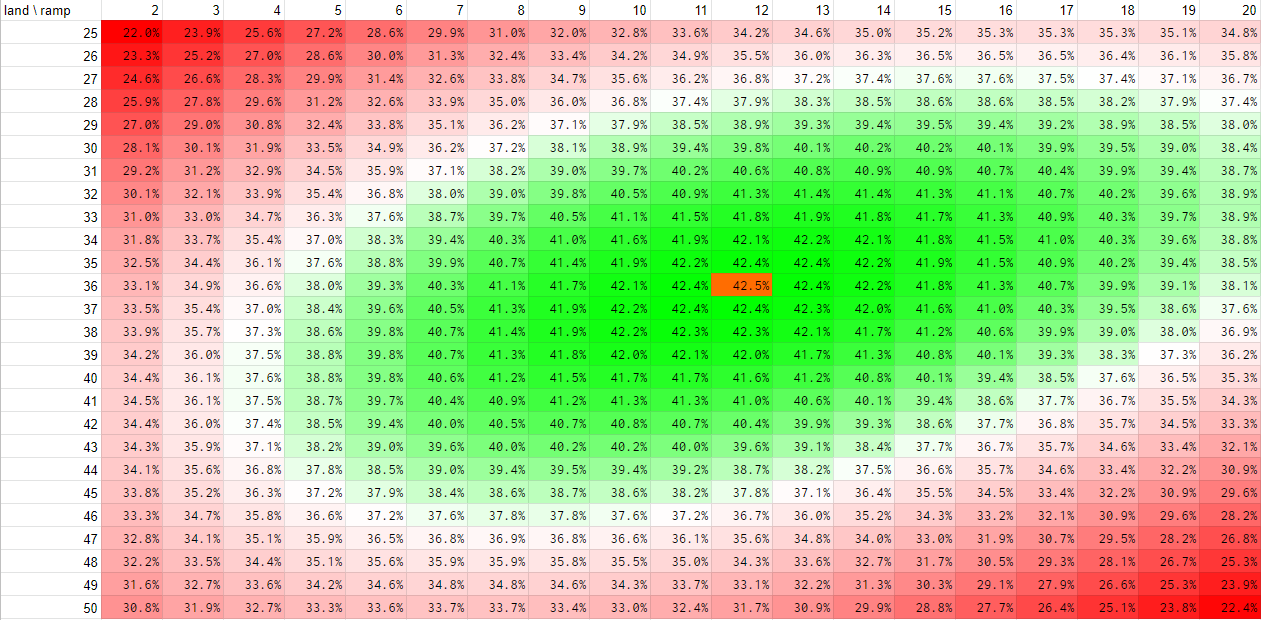
Here's a cool heat map. Look at it. It's amazing. This heat map describes the probability of drawing a good opener and then having two favourable draws on turns 1 and 2. Each cell simply means "probability of happy times". From it you can see that the optimum is 38 lands and 16 ramp spells but the probability doesn't decrease significantly if you go to 37 lands and 15 ramp spells (hence the title of the post). This is surprising because the old adage is that your deck should have about 36 lands and 10 ramp spells in it for a total of 46 mana sources (my recommandation in the previous article was 36 and 12 for a total of 48). While it's close to that you may want to look at your deck critically and think if you need more than 50 sources. If you don't care about casting your commander on turn 3 then go with something lower. The "midpoint" of the colour scale is set to 85th percentile, by the way. So roughly green is good.

In more detail: each cell takes the probability of finding a particular kind of opener (outlined in the table above) and then multiplies that (the AND condition in probabilities) by the probabilities of good outcomes and then adds all the hands together (the OR condition in probabilities) to produce a single probability table. Each cell has a bunch of multivariate hypergeometric functions (not the simple kind) - it's a bit cumbersome so if you want more details about this you must contact me directly.

Fun fact: the table contains 11250 calculations where each calculcation has a number that is in the ballpark of 10 billion (American notation; 1010 for the more scientific minded people). It takes a few minutes to render the entire table.

Thank you for reading, hope this helps you somehow! Always take a stranger's word with a pinch of salt and feel free to disagree in the comments.

A small nod to further draws If we play 36 lands and 12 ramp spells our chance of drawing either a land or a ramp card as your first draw is a little under 50% (48/99). Over the course of the game this percentage should stay about the same regardless of how many cards we draw if we assume you're not an outlier i.e. being mana screwed or mana flooded. This roughly means that when you run out of mana in your opening hand (by turn 2 or 3) you will have drawn about 1-1.5 new sources. Play those too and you're looking at a total of 1.5-2 additional sources before you run out of mana sources completely.

Since finding a 4-mana opening hand rather than a 3-mana one is the more common option out of the two we can mostly assume that most decks will get to their magical 6 mana somewhat on curve, depending on luck. After that you'll get a mana source every second turn or so.

Limitations We've covered most of these on the way here but here's a recap.

This study only optimises your starting hand. It does not know anything about the future draws.

A deck contains 99 cards, a certain number of ramp spells and lands. These categories do not overlap and the calculations for example don't take into account the possibility of keeping a mana rich hand where one of the lands is actually a MDFC. Or Ancient Tomb.

An opening hand is 7 cards. Mulligans are London mulligans. We mulligan a maximum of 3 times - i.e. at worst you tuck 2 cards from your hand.

A ramp spells can only have mana values of 0, 1, or 2. This means that you can't really use the chart to figure out your available mana on the early turns because an Arcane Signet and [[Mana Crypt]] are of the same value in this study.

A keepable hand is on of the following: 2 lands and 1 ramp spell, 2 lands and 2 ramp spells, 3 lands, or 3 lands and 1 ramp spell. You might keep a different kind of a hand depending on the specific circumstances but they're not worth optimising for.

An additional variable would add a dimension making the data representation nearly impossible.

This tool breaks when you start drifting away from that average mana value of 3. This can be clearly seen in cEDH where a starting hand wouldn't look like the ones we drew. The scope of this study is not cEDH or ultra high mana value decks.

Conclusions Given our assumptions about an optimal hand the ideal amount of lands is 36 and the ideal amount of ramp is 12 spells. These numbers yield a very high chance of drawing into a good hand but small deviations from those numbers are usually almost as good. Can you cut a land for a cool new spell? Sometimes!

Future considerations One could argue that the opening hand isn't the most important aspect. In fact it could be hitting that magical 6 or 7 mana. The math gets a bit complicated because one needs to still decide what is a good opening hand, do mulligans and after all that draw the necessary cards to see how well a hand fares.

Feedback, please Did I make any mistakes? The math has been verified by a handful of people (hence "we" in the text) but there's always a chance we all overlooked something. Did you enjoy this? Is it going to be helpful for you?

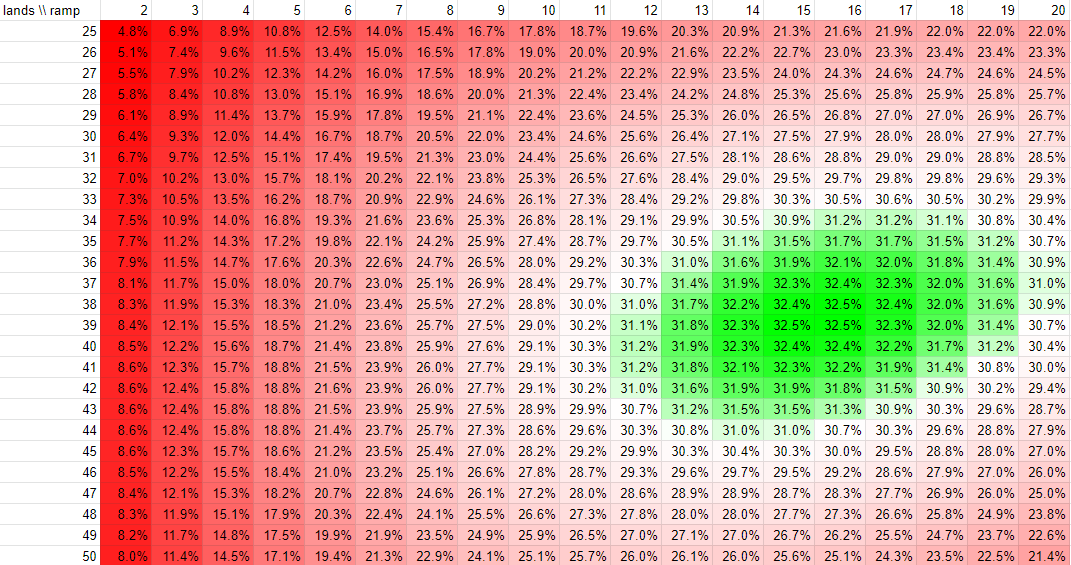
UPDATE Judging by the general feel of it I'm publishing one more chart. This chart here optimises additionally for 4 land hands, too. The formula I'm using breaks at 0 and 1 ramp spells and I can't be bothered to fix that because it's just an afterthought but as you can see if we optimise for these five opening hands:

2 lands, 1 ramp spell

2 lands, 2 ramp spells

3 lands, 0 ramp spells

3 lands, 1 ramp spell

4 lands, 0 ramp spells

the whole chart shifts dramatically to favour lands. The chart is for no mulligans (mulliganing doesn't change the optimum). It does make more hands keepable increasing the chance of getting "a good hand" but it warps the chart a lot.

This is one of the reasons why I did not include 4 land hands in the first place. The "ideal" would now be around 48-49 lands and about 0 ramp spells which does not make sense in the slightest. It doesn't reflect the power of ramp spells properly at all. All in all while 4 land hands may be keepable they're not really worth optimising for.

Show me the math already! A hypergeometric distribution is the statistical tool of choice this time. The first card you draw is always simple: if you have 40 lands and 99 cards the chance of drawing a land is 40/99. But what about after that? If you didn't draw a land the probability is 40/98 but if you did it's 39/98. How does that work? Hypergeometric distributions (Wikipedia article) describe this behaviour nicely when you've got a single variable. You need the following information: total number of cards, cards drawn, number of desired cards in the deck, and number of desired cards in the hand. Here's a tool you can use: the Aetherhub tool. The formula spits out a probability of the desired event happening, where "event" means for example "you drawing 3 lands in your opening 7 when you've got a deck of 99 cards with 40 lands in it".

There's a problem, though. What if we have lands and ramp we want to consider? Introducing multivariate hypergeometric distributions. A powerful tool that can have any number of variables. For example we could consider the probability of "you drawing 3 lands and 1 ramp spell and 1 draw spell in your opening 7 when you've got a deck of 99 cards with 40 lands in it". Multivariate hypergeometric distribution is what we're going to use. We've got two variables in this study: number of lands and number of ramp. We assume that the third category is "other spells" and none of these categories overlap (they're mutually exclusive). This puts things like [[Ancient Tomb]] in a weird spot because it belongs in two different categories simultaneously but we'll just blatantly ignore it.

Calculating the probability of a good hand We take P(2 lands, 1 ramp), P(2 lands, 2 ramp), P(3 lands, 0 ramp), and P(3 lands, 1 ramp) and we add those together to get P(good hand).

The way each calculation takes place is somewhat straightforward. In mathematics there is a concept called "combination" (Wikipedia article) which is what we're going to use since most programs don't understand multivariate hypergeometric distributions. It's written generally as "n choose k" where n is the total population of the item in question and k is the number of items in a subset. The number that is spat out is the number of combinations there can be. For example 3 choose 2 would be 3 because there are 3 different combinations of two numbers that can be represented with three numbers. Imagine an apple, an orange, and a pear. You can have an apple and an orange, an apple and a pear, or an orange and a pear - three combinations. Spreadsheet programs know combinatiorials by the function name "COMBIN(n,k)".

The formula for a multivariate hypergeometric distribution is the following: (lands choose desired number of lands in hand) x (ramp choose desired number of ramp in hand) x (the others choose desired number of other cards in hand) and the whole thing is divided by all the possible starting hands in EDH which is 99 choose 7. (Which is, by the way, a pretty big number.) The resulting number is the probability of drawing such a hand.

Mulligans Mulliganing in this case is easy. It's a bit of math but bear with me.

For the first hand it's just P(1st hand is good).

For the first mulligan since we're after the total chance we'll have P(1st is good) or P(1st is bad and 2nd is good) which is the same as P(1st is good) + P(1st is bad) x P(2nd is good).

Via complement this is the same as (1 - P(1st is bad)) + P(1st is bad) x (1 - P(2nd is bad)) which is the same as 1 - P(1st is bad) + P(1st is bad) - P(1st is bad) x P(2nd is bad).

Since between mulligans we always shuffle the deck these events are not dependent on each other i.e. they're independent. They're the same thing. Thus P(2nd is bad) is actually also P(1st is bad). At this point we're at 1 - P(1st is bad) + P(1st is bad) - P(1st is bad)^2.

This all nicely cancels itself out to the form 1 - P(1st is bad)^2 where "2" is actually the number of hands we've seen thus far. For the second mulligan it's 1 - (1st is bad)^3 and so forth.

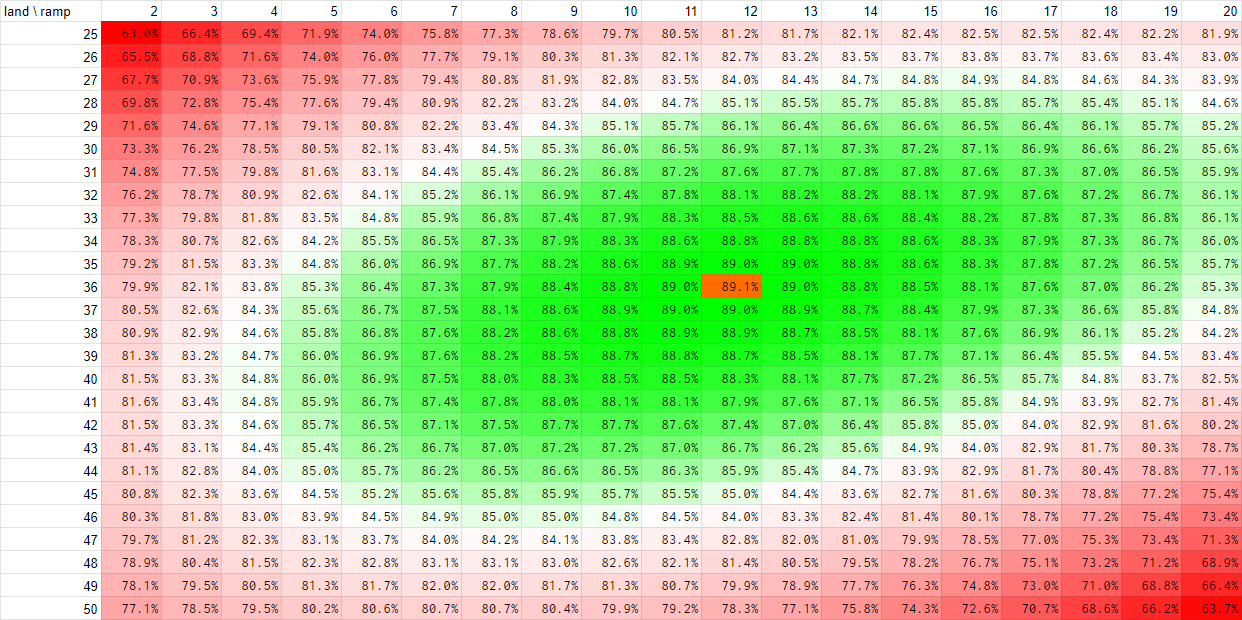
Opening hand breakdown Here are the coveted charts - the first one is for the case of no mulligans and the second one is with three mulligans.

On the chart you see a heat map. The leftmost column represents the number of lands and the topmost row represents the number of ramp spells. The percentages you see in the middle are the chance of you succeeding in drawing a good hand as outlined earlier.

Each probability you see on the first heat map is for just the opening hand. Each probability you see on the second heat map is for three mulligans, i.e. down to 5 cards. It's an arbitrary number but as you can see from the percentages it's pretty rare that we'd have to mulligan any further. Plus keeping a 4 card hand is not very lucrative because you need some lands and ramp but you don't really have any space for gas. You can also go ahead and keep a mana rich hand (e.g. a 4 land hand) and bottom some mana sources you don't need in the later mulligans so that increases your chances of finding a keepable hand significantly.

You can read the charts in many ways. The most obvious takeaway is the "optimal" composition at 36 lands and 12 ramp spells because the percentage of drawing into a successful hand is the highest at that point. Isn't that what people usually recommend?

One can also use it in two other ways: given that you have an X amount of lands or ramp how many of the other type should one run for the best results? The third way is to decide on a percentage you're willing to get screwed over and look up compositions that have the same number.

What's a good opening hand? Where did the early draws go? Worry not, the justification for why they're not that relevant is simple. A good opening hand has a good mixture of lands, ramp and gas which is exactly the same as good early draws: a good mixture of lands, ramp and gas.

A good mixture of lands, ramp and gas is a very philosophical question. Some prefer to have a safe opening hand, some prefer riskier hands and rely on further draws to get to their target amount of mana. Speaking of which: the average mana value of most decks hovers around 3, give or take ½. It's safe to assume that a deck wants to safely be able to play their 3-drops ahead of or on curve and then hit the crucial 6 or 7 mana as soon as possible to cast their biggest spells or cast two 3-drops per turn. After that point extra mana becomes largely irrelevant and most people prefer drawing either gas or draw spells which mostly eliminates the need to consider the distribution. (Extra draws will guarantee you will always hit your land drops late game.)

For the purposes of this study we settled on these options:

2 lands and 1 ramp spell

2 lands and 2 ramp spells

3 lands and 0 ramp spells

3 lands and 1 ramp spell

As you can notice we're mostly aiming for a situation where we have either 3 or 4 mana on turn 3, guaranteed.

None of this applies to cEDH where hand compositions are very different. That'll be a topic of its own.

Why can't I keep a 2 or 4 land hand? Most spells in an average deck (excluding ramp spells) cost 3 mana. Having just two lands is risky and while statistically you should be able to draw into an additional mana source soon you're risking missing land drops.

So what about 4 land hands? You must remember that you're playing on curve till turn 4 and you've only got 3 other cards in your hand. With 3 lands and 0 ramp you've got 4 other cards and you're not "flooded" on mana. With 3 lands and 1 ramp spell you indeed also have 3 cards in hand but this time you get to play your 4-drop on turn 3 already.

You may disagree with us and that is okay. Under certain circumstances almost anything can be a good hand and we agree with you on that. Not all decks run the same way. As it was established before this is more of a philosophical question than an actual fact. This is a rough approximation of what could be a good hand in an average deck.

A quick rundown of how probabilities work In probabilities we consider events and the likelyhoods of such events happening. If you have an event A and an event B and you want both of those to happen you multiply the numbers. If you have the same events but you want either one of them to happen you add the numbers. The probability of rolling a 6 on a d6 is 1/6. We roll two d6s and we want the first one of them to be a 6 and the second to be a 5. We multiply the events: 1/6 x 1/6 to get 1/36. If we don't care which one of them is a 5 and which one is a 6 we can add the events of rolling "a 6 and a 5" and "a 5 and a 6". This way: 1/6 x 1/6 + 1/6 x 1/6 = 2/36 (which is the same as 1/18).

For future reference we're going to occasionally use the "P()" notation to describe events. For example "P(rains tomorrow)" reads "the probability that it rains tomorrow".

I have done some research into this. I will be an absolute rudebag and copy and paste my own findings here. Formatting will be broken and I can't be bothered to fix it. Sorry about that.

TL;DR LOTS OF TEXT, YO.

(They're still available on Reddit if anyone wants to see the original posts. Ask for a link.)

FIRST POST:

TL;DR: You should have 36 lands and 12 ramp spells in your deck.

PSA: I added an update (at the very bottom of the post) that handles the case of accepting 4 land hands and optimising for them. Check it out.

How is this different from everything else people post on this sub? This approach considers mulligans.

This approach considers calculated probabilities.

This post isn't a Monte Carlo simulation.

This post isn't from personal experience.

This approach outlines its limitations clearly.

What are we trying to figure out? Ultimately this short study aims to give a perspective to lands and ramp in EDH. What is the optimal amount of lands and ramp one should have in a deck? As you will find out in more detail soon that is an impossible question in the sense that it needs extra definitions. Our goal here is to figure out some reasonable definitions for what constitutes "an optimal amount" and refine the question.

Let's get to work. "An optimal number" has roughly three components: what's a good opening hand, what are good early/mid game draws and how does one eliminate dead land draws late game. I can already tell you that the last part is impossible with regular probability math or at best so long that nobody would ever read it. Our focus will mainly be on the opening hand because that is the one time you get to see a huge portion of your deck. If you mulligan twice you've already seen 21 cards from your deck which is more than many people draw over the course of the rest of the game. Emphasis should be placed on shaping a good opening hand.

What is a ramp spell? A ramp spell is something that puts you ahead of the "curve" i.e. the mana you'd have available if you were playing lands only. There are many kinds of ramp spells: Llanowar Elves is a "dork" i.e. a creature that produces mana. Arcane Signet is a "rock" i.e. an artifact that produces mana. Rampant Growth is a ramp spell that puts a land from your deck onto the battlefield.

For the purposes of this study we consider a ramp spells to cost 2 or less mana. Not really important for our statistics but provides a basis for what we consider to be a good opening hand.